【python】ヒストグラムと確率密度関数を重ねる方法

はじめに

データの分析や、データの可視化を行う際にヒストグラムだけでは分布形状がわかりづらいので、確率密度関数を重ねて描画したいことがあるかと思います。
製造業の場合は、工程の品質評価用に寸法のばらつき等を見たい/示したいときによく使います。

私の所属する会社でも、ゴリゴリに作られたエクセル帳票があり、そこに測定データを入れるとヒストグラムと確率密度関数が重ねて書けるようになってます。
ただ、そんな帳票を解読したり、使わなくてもpythonでは比較的簡単に作れますので、今回はその方法について解説していきます。
以下のような図を作ります。

注意点

今回は分布の形状が正規分布であると言える(言えないとは言い切れない)データを対象としています。
分布形状がわからないものや正規分布でないものは、尤もらしい確率密度関数が得られないので使用には注意が必要です。
次回は分布形状がわからないときの方法について説明予定です。

はじめに
- 注意点
コード、解説
正規分布ではないデータの場合
- 母集団が複数混ざっているとき
- 正規分布でない分布に従っているとき
終わりに
- 分布等の統計学の勉強について

コード、解説

それでは順を追ってコードを実装していきます。

ヒストグラムの描画

まずは、正規分布に従うデータを用意します。
本当は測定データ等をここで使いますが、今回は何もないのでランダムにデータを作成します。
ある分布に従うデータの作成にはscipy.statsを使用します。
Statistical functions (scipy.stats) — SciPy v1.11.4 Manual

正規分布に従うランダムデータを作成し、ヒストグラムを描画してみます。

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.stats import norm
sns.set()

# 正規分布に従うデータのサンプルを作成
# 平均10, 標準偏差1の正規分布に従うランダムデータを1000個
data = norm.rvs(loc=10, scale=1, size=1000)
print(type(data))  # 戻り値はnp.array

fig, ax = plt.subplots()
ax.hist(data, density=True, label='data')
ax.legend()
ax.set_xlim(5, 15)
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('density')
plt.show()

結果は以下です。

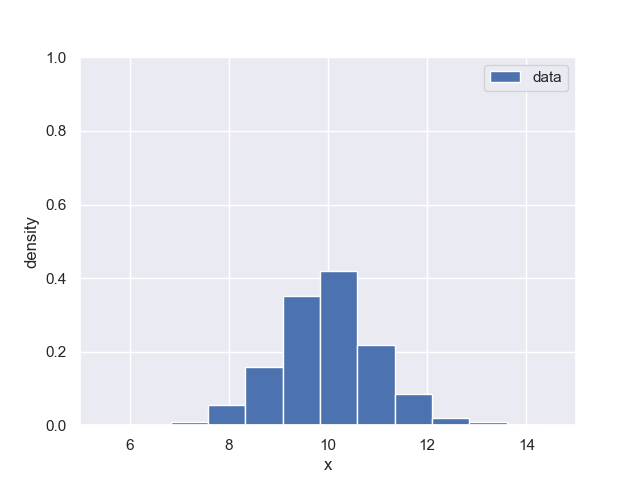
まず初めに、seabornというモジュールをインポートしてsetしています。
これはmatplotlibのグラフの見た目をいい感じにおしゃれにしているだけの操作ですのであんまり関係ありません。

import seaborn as sns
sns.set()

正規分布に従うランダムデータの生成には下記コードを使用します。
引数にはloc(期待値(平均)), scale(標準偏差), size(データ個数)を指定します。

data = norm.rvs(loc=10, scale=1, size=1000)

従う分布を変えるときはnormを別の分布の名前にするだけです。
Statistical functions (scipy.stats) — SciPy v1.11.4 Manual

ヒストグラムは下記コードで描画していますが、確率密度関数と値のスケールを合わせるためにdensityプロパティを指定して値を正規化しています。

fig, ax = plt.subplots()
ax.hist(data, density=True, label='data')
plt.show()

正規化って何という感じだと思いますが、ヒストグラムの棒グラフすべて足し合わせた面積が1になるようにデータのスケールを合わせます。
データが $x$ になる確率 $f(x)$ が確率密度関数であり、確率密度関数も積分すると1になることから正規化したヒストグラムとスケールが合います。

確率密度関数の導出

正規分布における確率密度関数 $f(x)$ は下記になります。

$f(x) = \dfrac{1}{\sqrt{2\pi}\sigma}\exp{(-\dfrac{(x - \mu)^{2}}{2\sigma^{2}})}$

ここで、 $\sigma$ は標準偏差、 $\mu$ は平均を表します。

正規分布に従うデータの標準偏差及び平均は以下のコードで取得できます。

# 確率密度関数のパラメータ取得
data_mean = np.mean(data)   # 平均
data_std = np.std(data)     # 標準偏差

上のパラメータ及び数式を用いて、確率密度変数は以下のようにもとめることができます。

# 確率密度関数描画用のx軸データ
x = np.linspace(5, 15, 1000)

# 確率密度関数の値を取得
y = np.exp(- (x - data_mean) ** 2 / (2 * data_std ** 2)) \
            / (np.sqrt(2 * np.pi) * data_std)

ただ、上記数式を覚えたり、実装するのはなかなかに大変なのでscipyのモジュールを使います。
以下で同様の処理が行えます。

# 確率密度関数の値を取得
y = norm.pdf(x, loc=data_mean, scale=data_std)

ヒストグラムと確率密度関数を重ねて表示

ここまで出来たらあとはプロットするだけです。
先のヒストグラムを表示したコードに確率密度関数をプロットしてあげるだけです。

全コードは以下です。

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.stats import norm
sns.set()

# 正規分布に従うデータのサンプルを作成
# 平均10, 標準偏差1の正規分布に従うランダムデータを1000個
data = norm.rvs(loc=10, scale=1, size=1000)
print(type(data))  # 戻り値はnp.array

# 確率密度関数のパラメータ取得
data_mean = np.mean(data)   # 平均
data_std = np.std(data)     # 標準偏差
print(data_mean, data_std)

# 確率密度関数描画用のx軸データ
x = np.linspace(5, 15, 1000)

# 確率密度関数の値を取得
y = norm.pdf(x, loc=data_mean, scale=data_std)

fig, ax = plt.subplots()
ax.hist(data, density=True, label='data')
ax.plot(x, y, label='pdf')
ax.legend()
ax.set_xlim(5, 15)
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('density')
plt.show()

実行結果は下記の通り。

正規分布ではないデータの場合

冒頭に正規分布のデータが対象といいましたが、正規分布でないデータで実施したらどうなるか見てみましょう。
いくつか例としてデータを作成してみてみます。

母集団が複数混ざっているとき

各々の母集団は正規分布に従っていますが、それがサンプルに複数混ざっている時を例として考えます。
今回は以下を考えましょう。
サンプルの内訳：

平均10, 標準偏差1の正規分布に従う母集団から700個サンプリングしたもの
平均5, 標準偏差2の正規分布に従う母集団から300個サンプリングしたもの

サンプルの生成コードは以下です。

# サンプル生成
data1 = norm.rvs(loc=10, scale=1, size=700)    # 母集団1
data2 = norm.rvs(loc=5, scale=2, size=300)    # 母集団2
data = np.concatenate([data1, data2])    # サンプルを混ぜ合わせ
print(len(data))   # 2つの母集団からの合計1000個のサンプルデータ

これでヒストグラムと確率密度変数をプロットしてみますと下記のようになります。

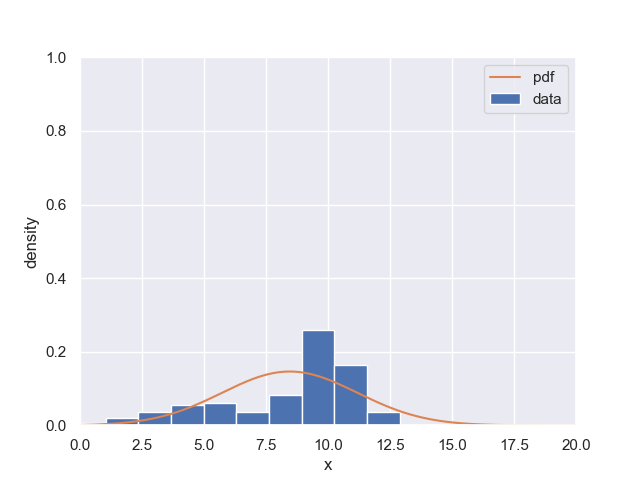
ヒストグラムと、確率密度変数の形が全くあっていないので確率密度変数の値は信用できないと言えます。

正規分布でない分布に従っているとき

例として母集団がベータ分布に従っている時を考えます。
ベータ分布に従うサンプルは下記コードで作成できます。

from scipy.stats import beta
data = beta.rvs(2, 9, size=1000)

これでヒストグラムと確率密度変数をプロットしてみますと下記のようになります。

こちらも、ヒストグラムと確率密度変数があまりあってないように見えますね。

終わりに

正規分布とわかっているデータに対して、ヒストグラムと確率密度関数を表示する方法について解説しました。
次回以降、分布形状がわからない場合について解説記事書く予定です。

ランキング参加中

プログラミング

分布等の統計学の勉強について

大学で統計はあまりやってこなかったんですが、製造業ならではの工程の品質管理やら、機械学習やらを扱うにあたって勉強しておくに越したことはないので社会人になってから勉強を始めました。

入門には以下の書籍が参考になりました。
あまり数式も出てこず、どういうときに統計学の何が使えるか？みたいなことが物語形式でまとめられてますのであまり苦痛を感じず勉強できました。

リンク

また、pythonを使ったデータ分析について下記が体系化されていてわかりやすかったです。
統計や確率の基礎から機械学習まで網羅されていました。
pythonに関してもnumpy, pandas, scipy, matplotlibの使い方も丁寧に解説されており参考になります。

リンク

morikomorou’s blog

自分が学んだことなどの備忘録的なやつ