はじめに
今回はpythonでフーリエ変換(FFT)をやっていきます。
フーリエ変換は信号データ等の周波数特性を調べる際によく使います
割と簡単に実装できるのでやってみます。
詳しい数式等は省きます。
サンプルデータの作成
今回はサンプルとして100Hzと350Hzの正弦波を足し合わせた信号を作成します。
サンプリング周波数は10kHz。
サンプル数は1024とします。
高速フーリエ変換(fft)ではサンプル数が2の累乗の時に最も高速に計算できるようになっているのでサンプル数は2の累乗の数とします。
import numpy as np import matplotlib.pyplot as plt N = 1024 # サンプル数 dt = 0.0005 # サンプリング周期 [s] f1, f2 = 100, 350 # 周波数 [Hz] t = np.arange(0, N * dt, dt) # 時間 [s] x = 1.5 * np.sin(2 * np.pi * f1 * t) + np.sin(2 * np.pi * f2 * t) # データ fig, ax = plt.subplots() ax.plot(t, x) ax.set_xlabel("Time [s]") ax.set_ylabel("Signal") ax.grid() plt.show()
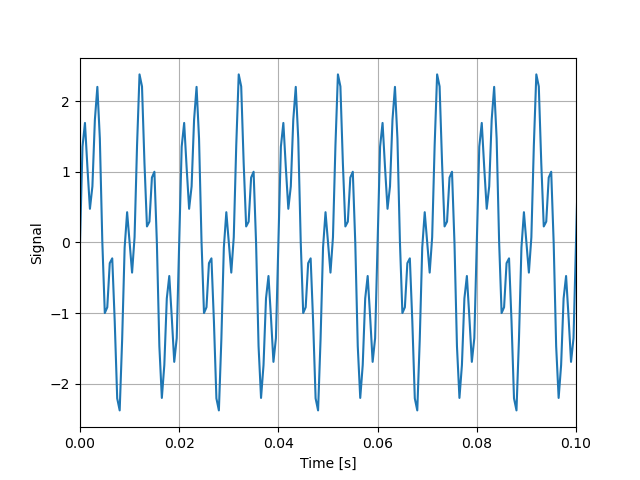
このデータからどういう周波数の振動成分が含まれているのか調べるのに使用するのがフーリエ変換です。
詳しくは下記書籍が参考になります。
フーリエ変換の実装
numpyのfftパッケージを使用します。
関数numpy.fft.fft()で簡単にフーリエ変換を行えます。
周波数軸はnumpy.fft.fftfreqで取得できます。
F = np.fft.fft(x) # フーリエ変換 freq = np.fft.fftfreq(N, d=dt) # 周波数スケール
振幅スペクトルの取得
振幅スペクトルは信号をフーリエ変換した結果の絶対値をとったものです。
元の信号との大きさを合わせるために正規化も併せて行います。
サンプルデータ数によって大きさが変わってしまいますのでサンプルデータ数で割る処理です。
# フーリエ変換の結果を正規化 F = F / (N / 2) # 振幅スペクトル Amp = np.abs(F) fig, ax = plt.subplots() ax.plot(freq[:N//2], Amp[:N//2]) ax.set_xlabel("Frequency [Hz]") ax.set_ylabel("Amplitude") ax.grid() plt.show()

もともとサンプルデータとして振幅1.5周波数100Hzと振幅1周波数350の正弦波を足し合わせておりましたが、
このグラフでもぴったり100Hzと350Hzのところにピークが立っていることがわかります。
ただ、振幅に関しては1.4と0.9くらいで若干ずれがありますね。
パワースペクトルの取得
ついでにFFT解析でよく使うパワースペクトルも求めておきます。
これは振幅スペクトルの2乗なので簡単ですね。
# パワースペクトルの計算(振幅スペクトルの二乗) Pow = Amp ** 2 fig, ax = plt.subplots() ax.plot(freq[:N//2],Pow[:N//2]) ax.set_xlabel("Frequency [Hz]") ax.set_ylabel("Power") ax.grid() plt.show()

リーケージ誤差と窓関数について
FFT解析において気を付けないといけないのはリーケージ誤差というものです。
サンプルデータの開始点と終了点がずれているとそのずれが振動の一部となり、FFT解析時の誤差となってしまうということです。
先の振幅スペクトルでは以下の箇所がリーケージ誤差です。
ピークの裾野が広がってしまっています。
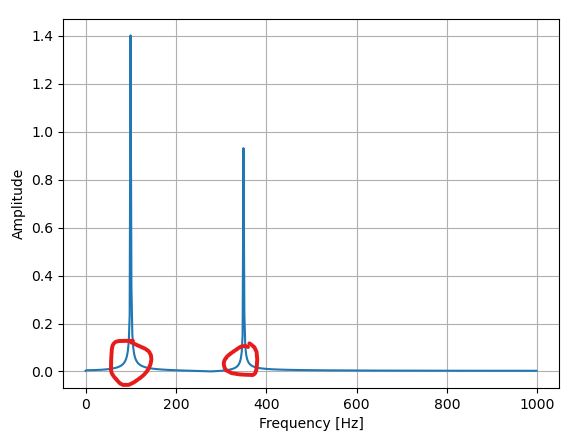
リーケージ誤差を小さくするために窓関数というものを使用します。
よく使われるのはハニング窓関数です。
ハニング窓関数
scipy.signal.hannパッケージを使用すれば一発です。
from scipy import signal window = signal.hann(N) # ハニング窓関数 fig, ax = plt.subplots() ax.plot(t, window) ax.set_xlabel("Time [s]") ax.set_ylabel("Amplitude") ax.grid() plt.show()
以下のように、サンプルデータの開始点と終了点でゼロとなる形をしている関数です。
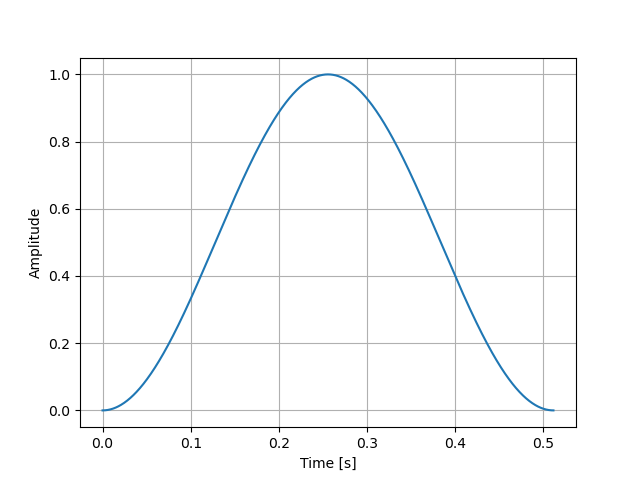
窓関数は元の信号と掛け合わせて使用します。
fig, ax = plt.subplots() ax.plot(t, x * window) ax.set_xlabel("Time [s]") ax.set_ylabel("Amplitude") ax.grid() plt.show()
窓関数を掛け合わせたサンプルデータは下記のようになります。
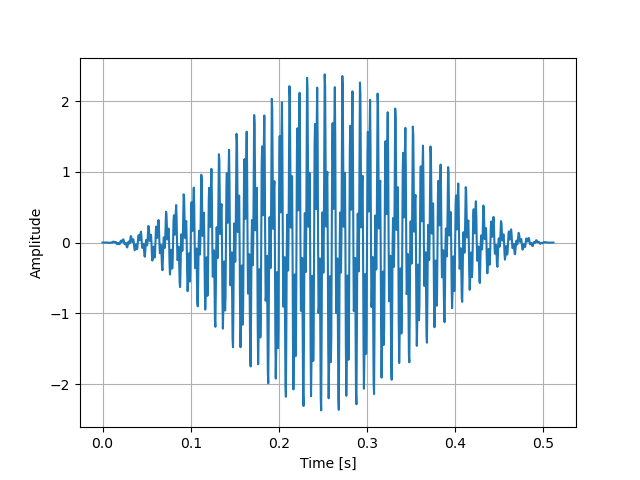
これで周波数成分を壊すことなくサンプルデータの開始点、終了点間のずれをゼロにできます。
ハニング窓関数を使ったFFT解析
先ほど作成したサンプルデータを使ってもう一度FFTを行ってみます。
# 高速フーリエ変換 F = np.fft.fft(x * window) freq = np.fft.fftfreq(N, d=dt) # 周波数スケール # フーリエ変換の結果を正規化 F = F / (N / 2) # 窓関数による振幅減少を補正する F = F * (N / np.sum(window)) # 振幅スペクトル Amp = np.abs(F) fig, ax = plt.subplots() ax.plot(freq[:N//2], Amp[:N//2]) ax.set_xlabel("Frequency [Hz]") ax.set_ylabel("Amplitude") ax.grid() plt.show()
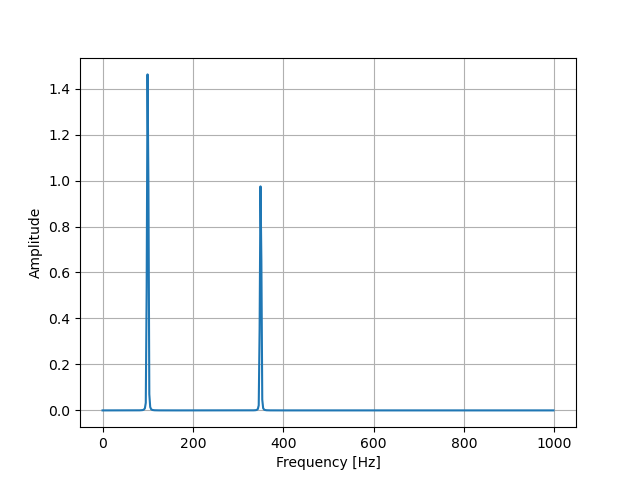
裾野が狭くなり、リーケージ誤差が小さくなっていることがわかります。
振幅の値もほぼ1.5と1.0となり、元の波形データに近づきました。
窓関数をかけると、振幅が小さくなってしまいますので、その分補正を入れています。
ハニング窓関数を積分した値とサンプル数の比率分振幅が検証してしまいますので、ハニング窓関数の積分値をサンプル数で割った値の逆数をかけて補正します。
おわりに
ライブラリをつかって簡単にFFT解析を行う方法について解説しました。