【python】カーネル密度推定による確率密度関数の推定

初めに

以前の記事で正規分布に従うデータについて、確率密度関数を求めてヒストグラムと一緒に描画する方法について説明しました。

今回は、分布がわからないデータのときに確率密度を推定して、ヒストグラムと重ねる方法について紹介します。

このような感じになります。

初めに
カーネル密度推定とは？
ヒストグラムとカーネル密度推定結果を重ねる
終わりに
- 分布等の統計学の勉強について

カーネル密度推定とは？

サンプルデータから、全体の分布形状を推定するための手法です。
ヒストグラムもその一種です。
サンプルデータ一つ一つの値に広がりを持たせて足し合わせることで、サンプルデータ間の確率密度を補完します。

どういう時に使うか？

データの母集団のの確率密度関数を推定しますので、ある値からある値までの範囲にどれくらいの確率で値が存在するか等の予測が可能です。

定義

$x_{1}, x_{2}, ..., x_{n}$ をサンプルデータの値としたときに、カーネル密度推定量 $f(x)$ は以下の式で表すことができます。

$f(x) = \dfrac{1}{n}\sum^{n}_{i=1}\dfrac{1}{h}K\left(\dfrac{x - x_{i}}{h}\right)$

$h$ はバンド幅と呼ばれ、1つのデータの周りへの影響度合いを決めるパラメータです。
ここで $K(u)$ はカーネル関数と呼び、よく使われるのが以下の式で表されるガウス関数です。

$K(u) = \dfrac{1}{\sqrt{2\pi}}\exp{\left(-\dfrac{u^{2}}{2}\right)}$

ここで、カーネル関数としてガウス関数を使用した際に、 $u = x - x_{i} / h$ をカーネル密度推定の式に代入すると以下の形になります。

$f(x) = \dfrac{1}{n}\sum^{n}_{i=1}\dfrac{1}{\sqrt{2\pi}h}\exp{\left(-\dfrac{(x - x_{i})^{2}}{2h^{2}}\right)}$

サイズ $1/n$ 、平均 $x_{i}$ 、標準偏差 $h$ の正規分布を足し合わせた形となってますね。
正規分布の確率密度関数の積分値は1なので、それを $1/n$ したものを $n$ 個足し合わせるので、求められるカーネル密度推定量も積分したら1となります。

カーネル密度推定を行ってみる

試しに少量のサンプルで上記の実装をしてみましょう。
サンプルデータとして以下のデータを使います。

data = [5, 6, 8, 9, 10, 12]

サイズ $1/n$ 、平均 $x_{i}$ 、標準偏差 $h$ の正規分布の確率密度関数(カーネル関数)を描いてみます。
標準偏差 $h=1$ でやってみます。

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.stats import norm
sns.set()

data = [5, 6, 8, 9, 10, 12]
h = 1
n = len(data)

# 確率密度関数描画用のx軸データ
x = np.linspace(0, 20, 1000)

# 確率密度関数の値を取得
ys = []
for x_i in data:
    ys.append(norm.pdf(x, loc=x_i, scale=h) / n)

fig, ax = plt.subplots()
for i in range(len(ys)):
    ax.plot(x, ys[i], 'k--', linewidth=0.5)
ax.set_xlim(0, 17.5)
ax.set_ylim(0, 0.2)
ax.set_xticks(data)
ax.set_xlabel('x')
ax.set_ylabel('density')
plt.show()

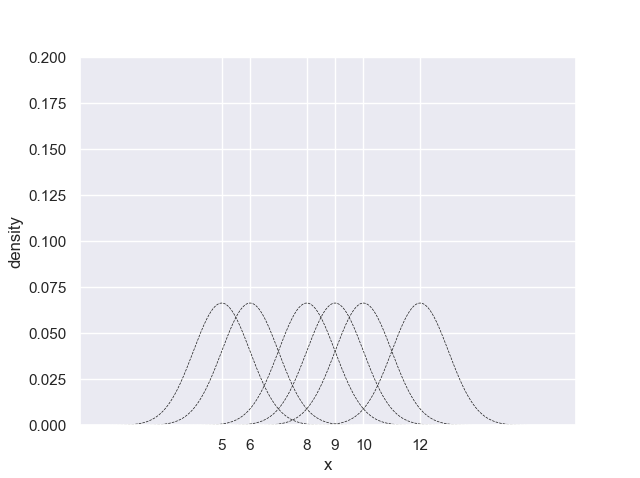
カーネル関数を全て足し合わせると以下の形になります。

sumy = np.sum(ys, axis=0)
fig, ax = plt.subplots()
for i in range(len(ys)):
    ax.plot(x, ys[i], 'k--', linewidth=0.5)
ax.plot(x, sumy)
ax.set_xlim(0, 17.5)
ax.set_ylim(0, 0.2)
ax.set_xticks(data)
ax.set_xlabel('x')
ax.set_ylabel('density')
plt.show()

イメージはつかめましたか？
データが密集している部分ほどカーネル関数が重なり合っていて、その足し合わせである密度推定量は大きくなっていることがわかります。

ヒストグラムとカーネル密度推定結果を重ねる

先ほどは1つ1つのデータのカーネル関数を求めて足し合わせましたが、scipy.statsのライブラリには1発でできるものが実装されております。
ガウス関数を使用したカーネル密度推定がgaussian_kde()というもので実装されています。
scipy.stats.gaussian_kde — SciPy v1.11.4 Manual

実際に使ってみましょう。
データは前回使った以下2つの母集団からサンプルをとったデータとします。

平均10, 標準偏差1の正規分布に従う母集団から700個サンプリングしたもの
平均5, 標準偏差2の正規分布に従う母集団から300個サンプリングしたもの

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.stats import norm, gaussian_kde
sns.set()

# サンプル生成
data1 = norm.rvs(loc=10, scale=1, size=700)    # 母集団1
data2 = norm.rvs(loc=5, scale=2, size=300)    # 母集団2
data = np.concatenate([data1, data2])    # サンプルを混ぜ合わせ

# 確率密度関数描画用のx軸データ
x = np.linspace(0, 20, 1000)

# gaussian_kdeのインスタンスを生成
kde = gaussian_kde(data)

# カーネル密度推定
y = kde(x)

fig, ax = plt.subplots()
ax.hist(data, density=True, label='data')
ax.plot(x, y, label='kde')
ax.legend()
ax.set_xlim(0, 20)
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('density')
plt.show()

結果は以下です。

真の分布と比べてみましょう。

# 真の分布
true_y = norm.pdf(x, loc=10, scale=1) * 0.7 \
        + norm.pdf(x, loc=5, scale=2) * 0.3

fig, ax = plt.subplots()
ax.hist(data, density=True, label='data')
ax.plot(x, y, label='kde')
ax.plot(x, true_y, label='true_pdf')
ax.legend()
ax.set_xlim(0, 20)
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('density')
plt.show()

若干形状が異なりますが、ピークは一応当たってますね。
scipy.statsのgaussian_kdeでは、bw_methodプロパティを指定することでバンド幅も設定できます。
デフォルトではデータからいい感じにバンド幅を決めてくれています。
スコットルールというもので決めているようです。
試しに0.1にしてみます。

# gaussian_kdeのインスタンスを生成
kde = gaussian_kde(data, bw_method=0.1)

すごくよくあてはまりましたが、真の分布は常にわかっているわけではないので、
あまりいじらないほうがよいでしょう。

終わりに

正規分布ではないデータや、分布形状がわからないに対して、分布を推測する方法について説明しました。

ランキング参加中

プログラミング

分布等の統計学の勉強について

大学で統計はあまりやってこなかったんですが、製造業ならではの工程の品質管理やら、機械学習やらを扱うにあたって勉強しておくに越したことはないので社会人になってから勉強を始めました。

入門には以下の書籍が参考になりました。
あまり数式も出てこず、どういうときに統計学の何が使えるか？みたいなことが物語形式でまとめられてますのであまり苦痛を感じず勉強できました。

リンク

また、pythonを使ったデータ分析について下記が体系化されていてわかりやすかったです。
統計や確率の基礎から機械学習まで網羅されていました。
pythonに関してもnumpy, pandas, scipy, matplotlibの使い方も丁寧に解説されており参考になります。

リンク

morikomorou’s blog

自分が学んだことなどの備忘録的なやつ