【python】matplotlibでフラクタル図形(コッホ曲線)を描く

フラクタル図形について

皆さんはフラクタル図形ってご存知ですか？
私は大学の数学の授業で初めて知りました。
Wikipediaで調べてみると、図形の部分と全体が自己相似になっているものの事だそうです。
何言ってるのかよくわかりませんが、簡単に言うと拡大しても拡大しても複雑な図形のことだそうです。
ja.wikipedia.org

スーパーでたまに見かけるあの野菜もすっごくフラクタルです。

大学生の時フラクタルの授業受けた後、食堂で見かけて納得したのを思い出します。

本記事ではpythonでmatplotlibをつかってフラクタル図形を描いてみたいと思います。

今回はコッホ曲線を描いていきたいと思います

コッホ曲線とは？

下記のような図形のことを言います。

コッホ曲線

一見すごく複雑そうですが、単純なルールに基づいて書かれています。
各線分を3等分して、その真ん中の2点を頂点とする三角形を繰り返し描いていくだけです。

再帰関数について

フラクタル図形を描く前に、再帰関数について少し説明します。
フラクタル図形は、同じルールに則って繰り返し描写することで描けるものが多く、再帰関数を使うのが便利です
再帰関数とは関数内で自分を呼び出す関数のことで、再帰的に繰り返す処理に使えます。
pythonで書くと下記のような感じです。

def func(x):
    print(x)
    func(x + 1)

これは引数のxを1ずつ増やして繰り返し出力するコードですが、このままだと無限ループになってしまいます。
ですので、再帰関数には必ず下記のようにループを抜ける処理を入れる必要があります。

def func(x):
    if x > 10:
        return
    print(x)
    func(x + 1)

func(0)

# output ############
# 0
# 1
# 2
# 3
# 4
# 5
# 6
# 7
# 8
# 9
# 10

上の例のように自分を呼び出す前にprint文を書くと、行きがけ順に出力します。
プログラムのフローとしては下図のようなイメージです。

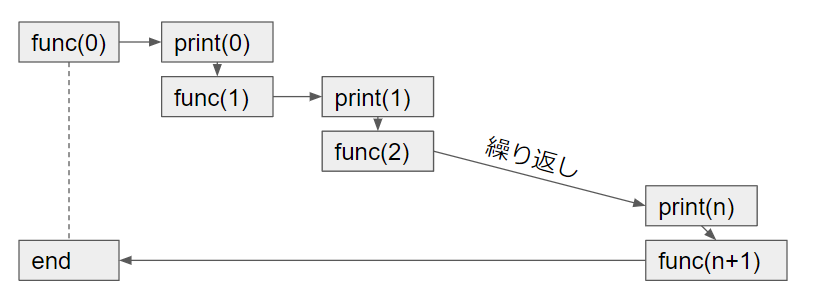
帰りがけ順に出力したいときはprint文を自分を呼び出した後にもっていきます。

def func2(x):
    if x > 10:
        return
    func2(x + 1)
    print(x)

func2(0)
# 10
# 9
# 8
# 7
# 6
# 5
# 4
# 3
# 2
# 1
# 0

こちらの場合はプログラムのフローは以下のようになります。

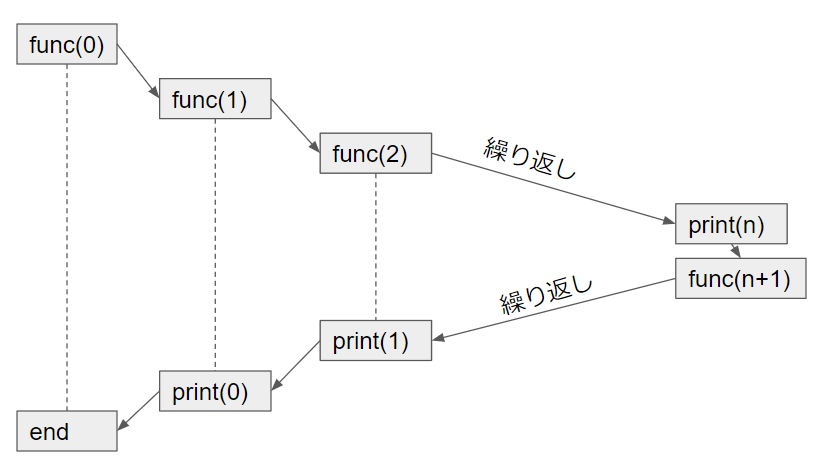
それではこれをもとにコッホ曲線を描いていきましょう

コッホ曲線の数式化

点, 点間の線分を考えます。

点の座標を、点の座標をと表すことにすると、それを3等分した2点とそれを頂点とした正三角形のもう一つの頂点の座標は下記のように求めることができます。

この計算を次は線分それぞれに対して同様に行います
この作業を回繰り返したものが深さのコッホ曲線となります。

コッホ曲線を描く

それでは上記の数式をもとにコッホ曲線を描くコードを書いていきましょう
コードは下記です。

import numpy as np
import math
import matplotlib.pyplot as plt

th = math.pi * 60 / 180   # 正三角形の角度をラジアン化
a = (0.0, 0.0)
b = (100.0, 0.0)
n = 5  # 繰り返し数
points = [a]  # 各点の座標を入れておくリスト(最終的にこれをプロット)


def koch(a, b, n):
    if n == 0:
        return
    s = (a[0] + (b[0] - a[0]) / 3, a[1] + (b[1] - a[1]) / 3)
    t = (a[0] + (b[0] - a[0]) * 2 / 3, a[1] + (b[1] - a[1]) * 2 / 3)
    u = (s[0] + (t[0] - s[0]) * math.cos(th) - (t[1] - s[1]) * math.sin(th),
         s[1] + (t[0] - s[0]) * math.sin(th) + (t[1] - s[1]) * math.cos(th))
    koch(a, s, n - 1)
    points.append(s)
    koch(s, u, n - 1)
    points.append(u)
    koch(u, t, n - 1)
    points.append(t)
    koch(t, b, n - 1)


koch(a, b, n)
points.append(b)
x = [points[i][0] for i in range(len(points))]
y = [points[i][1] for i in range(len(points))]
plt.plot(x, y, linewidth=0.5)
plt.axis('equal')
plt.savefig('Koch1.png')

このコードで以下のような図形が書けます。

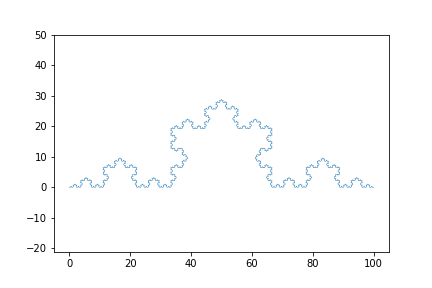
繰り返しのnの値をいろいろ変えてみると面白いです。

コード説明

再帰関数を使うと短いコードで書けます。
koch関数は引数に、分割したい線分の始点と終点の座標及び、残りの繰り返し回数を入れます。
最終的に1本の線にしたいので始点から順番に頂点の座標をリストに入れていく関数として定義しています。

koch関数内のコードを順番に見ていきます。

if n == 0:
    return

この部分はループを抜ける処理です。

s = (a[0] + (b[0] - a[0]) / 3, a[1] + (b[1] - a[1]) / 3)
t = (a[0] + (b[0] - a[0]) * 2 / 3, a[1] + (b[1] - a[1]) * 2 / 3)
u = (s[0] + (t[0] - s[0]) * math.cos(th) - (t[1] - s[1]) * math.sin(th),
       s[1] + (t[0] - s[0]) * math.sin(th) + (t[1] - s[1]) * math.cos(th))

この部分で、引数に指定した線分間の正三角形の頂点の座標を求めています

最後に再帰の部分です。

koch(a, s, n - 1)
points.append(s)
koch(s, u, n - 1)
points.append(u)
koch(u, t, n - 1)
points.append(t)
koch(t, b, n - 1)

この部分の考え方ですが、下図のように考えます。

koch(a, s, n-1)が線分間の深さn-1以下の頂点をすべて順番にリストに入れてくれる関数と想定して、そのあとに点の座標をリストに加えます。
次の線分も同様にkoch(s, u, n-1)の後に点の座標をリストに加えます。
残りの線分に関しても同様です。
なんか黒魔術チックですが、これでちゃんと動きます。

コッホの雪片も描いてみる。

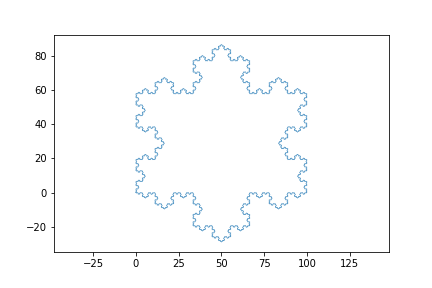
雪の結晶みたいでかっこいいですよね。
これも簡単で、最初の図形を直線ではなく正三角形にすれば同様に描けます。
コード載せておきます。

a = (0.0, 0.0)
b = (50.0, 100.0 * math.sin(th))
c = (100.0, 0.0)
n = 5
points = [a]
koch(a, b, n)
points.append(b)
koch(b, c, n)
points.append(c)
koch(c, a, n)
points.append(a)
x = [points[i][0] for i in range(len(points))]
y = [points[i][1] for i in range(len(points))]
plt.plot(x, y, linewidth=0.5)
plt.axis('equal')
plt.savefig('Koch2.png')

リンク