
はじめに
前回から本格的に4角形1次要素の平面応力状態における静弾性問題の有限要素解析の実装を行い始めました。今回はその続きで有限要素法による変形解析まで行います。
実装の流れ
前回のおさらいで実装の流れは下記のとおりです。
- Dマトリクス
の算出
- Bマトリクス
の算出
- 要素剛性マトリクス
の算出
- 全体剛性マトリクス
の算出
- 連立方程式を解き、全節点の変位
を求める
このうち、全体剛性マトリクスの算出まで完了しました。
今回は最後のステップである全節点の変位を求めることをやっていきましょう
実装
以前の記事で作成したコードと、クラス要件をベースに実装を進めてます。
境界条件の指定
有限要素解析を行う上でまずは境界条件を設定する必要があります。節点の拘束や節点にかかる荷重等を設定して、それをもとに解析を行うからです。
節点の拘束と節点にかかる荷重はNodeクラスの中で設定できるように変数として持たせておきます。
class Node: """ Nodeのインデックス、座標および境界条件をまとめておくクラス(2次元用) Attributes: id (int): Nodeのインデックス番号(重複不可) x, y (float): Nodeのx, y座標 """ def __init__(self, idx, x, y): self.id = idx self.x = x self.y = y self.bc_dist = [None, None] # 節点拘束[x方向、y方向](None:拘束なし) self.bc_force = [0, 0] # 節点荷重[x方向、y方向] def __str__(self): return 'Node {}: x {}, y {}'.format(self.id, self.x, self.y)
今回は以下のような問題を考えたいと思います。
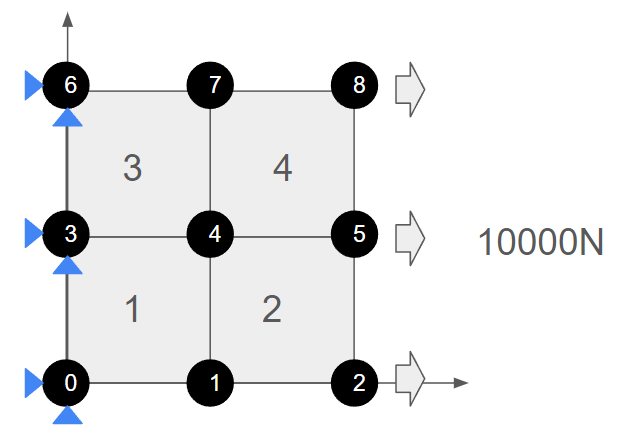
Node 0,3,6にはx,yの拘束を付与し、Node 2,5,8にはx方向に合計10000Nの荷重を与えます。
ここで荷重に関しては要素に対して均等に荷重がかかるよう節点に荷重を割り振る必要があります。
荷重がかかる要素は2と4の2つなので要素2,4には5000Nの荷重がそれぞれかかります。
要素2における荷重がかかる節点はNode2,5なのでNode2,5それぞれに2500Nの荷重がかかります。
要素4における荷重がかかる節点はNode5,8なのでNode5,8それぞれに2500Nの荷重がかかります。
よって、Node2,8には2500N、Node5には5000Nの荷重を節点荷重として与えておけば均等に10000Nの荷重が加わる状態となります。
それらを踏まえて上記の境界条件を設定してみます。
MESH_SIZE = 5 LENGTH = 10. HEIGHT = 10. THICKNESS = 1. E = 208000 # ヤング率 NU = 0.27 # ポアソン比 nodes_dict, elems = create_mesh(LENGTH, HEIGHT, MESH_SIZE, THICKNESS) mesh = Mesh(0, nodes_dict, elems) material = Material(E, NU) num_mesh_len = int(LENGTH / MESH_SIZE) num_mesh_hei = int(HEIGHT / MESH_SIZE) if num_mesh_len == 0: num_mesh_len = 1 if num_mesh_hei == 0: num_mesh_hei = 1 for k, v in mesh.nodes.items(): # x変位の境界条件を設定 if v.x == 0.0: v.bc_dist[0] = 0.0 # y変位の境界条件を設定 if v.x == 0.0: v.bc_dist[1] = 0.0 # 荷重の設定 if v.x == LENGTH and (v.y == 0.0 or v.y == HEIGHT): v.bc_force = [10000 / num_mesh_hei / 2, 0.0] elif v.x == LENGTH: v.bc_force = [10000 / num_mesh_hei, 0.0] for k, v in mesh.nodes.items(): print(v.id, v.bc_dist, v.bc_force)
0 [0.0, 0.0] [0, 0] 1 [None, None] [0, 0] 2 [None, None] [2500.0, 0.0] 3 [0.0, 0.0] [0, 0] 4 [None, None] [0, 0] 5 [None, None] [5000.0, 0.0] 6 [0.0, 0.0] [0, 0] 7 [None, None] [0, 0] 8 [None, None] [2500.0, 0.0]
先ほどの図の通り境界条件が設定できています。
境界条件の読み取り
ソルバー関数の中に上記で設定した境界条件を読み取る関数を作成しておきます。
その際に最終的に計算したい下記の式のも境界条件から読み取った荷重を埋めて作成します。境界条件で荷重の設定がない節点はいったん0で埋めておきます。
また、後々の計算のために変位拘束のあるノードの番号もまとめておきます。
class Solver: """ 有限要素法の計算を行うクラス Attributes: mesh (Mesh): Meshクラス material (Material): Materialクラス D (array 3x3): Dマトリクス """ def __init__(self, mesh, material): self.mesh = mesh self.material = material self.D = self.calc_D() def run(self): self.f, self.bc_dist_dict = self.read_boundary_cond() self.K = self.calc_K() ############ 略 ############### def read_boundary_cond(self): """ 境界条件を読み込み。 Returns: f (array 2node_num): 全体荷重ベクトル bc_dist_dict (dict): 全体変位ベクトルのうち、変位拘束のあるindをまとめた辞書 """ bc_dist_dict = {} f = [] for k,v in self.mesh.nodes.items(): f += v.bc_force if v.bc_dist[0] is not None: bc_dist_dict[k * 2] = v.bc_dist[0] if v.bc_dist[1] is not None: bc_dist_dict[k * 2 + 1] = v.bc_dist[1] return np.array(f), bc_dist_dict
連立方程式を解く
ここまで来たらあとは連立方程式を解くだけです。
class Solver: """ 有限要素法の計算を行うクラス Attributes: mesh (Mesh): Meshクラス material (Material): Materialクラス D (array 3x3): Dマトリクス """ def __init__(self, mesh, material): self.mesh = mesh self.material = material self.D = self.calc_D() def run(self): self.f, self.bc_dist_dict = self.read_boundary_cond() self.K = self.calc_K() self.d = self.solve() ############ 略 ############### def solve(self): for i in range(len(self.mesh.nodes) * 2): if i in self.bc_dist_dict.keys(): self.K[i, :] = np.zeros(len(self.mesh.nodes) * 2) self.K[:, i] = np.zeros(len(self.mesh.nodes) * 2) self.K[i, i] = 1.0 d = np.dot(np.linalg.inv(self.K), self.f.T) return d
ここで求まるdが全節点の変位量をまとめたベクトルとなります。
節点変位の可視化
節点変位ベクトルまで求まったので最後に変形を可視化して終わりにしましょう。
変形は微小なので倍率を指定して拡大表示できるようにしておきます。
class Solver: ############ 略 ############### def plot_deform(self, ratio=50): x = np.array([[node.x, node.y] for idx, node in self.mesh.nodes.items()]) x_new = x + self.d.reshape(len(self.mesh.nodes), 2) * ratio fig, ax = plt.subplots() for v in self.mesh.elements: patch = patches.Polygon(xy=v.xy, ec='black', alpha=0.3, fill=False) ax.add_patch(patch) for v in self.mesh.elements: xy_new = [(x_new[idx, 0], x_new[idx, 1]) for idx in v.node] patch = patches.Polygon(xy=xy_new, fc='red', ec='red', alpha=0.3, fill=False) ax.add_patch(patch) ax.autoscale() ax.set_aspect('equal', 'box') plt.show()
最後にこの全コードとプロットの結果を載せておきます。
import numpy as np import matplotlib.pyplot as plt from matplotlib import patches class Node: """ Nodeのインデックス、座標および境界条件をまとめておくクラス(2次元用) Attributes: id (int): Nodeのインデックス番号(重複不可) x, y (float): Nodeのx, y座標 """ def __init__(self, idx, x, y): self.id = idx self.x = x self.y = y self.bc_dist = [None, None] self.bc_force = [0, 0] def __str__(self): return 'Node {}: x {}, y {}'.format(self.id, self.x, self.y) class Element: """ 4角形1次要素Elementのインデックス、要素内のNode情報および要素の厚みをまとめておくクラス Attributes: id (int): Elementのインデックス番号(重複不可) node ([int, int, int, int]): 要素内のNodeのインデックスのリスト(左下から反時計回りで指定) thickness (float): Elementの厚み xy (ndarray(size: 2, 4)): Element内のNodeのxy座標まとめ """ def __init__(self, idx, node_idxs, thickness): self.id = idx self.node = node_idxs self.thickness = thickness self.xy = None def __str__(self): return 'Element {}: Nodes {}, Thickness: {}'.format(self.id, self.node, self.thickness) def get_coordination(self, nodes_dict): """ 要素の各節点のx,y座標を求めてself.xyに代入。 Args: nodes_dict ({Node.id: Node}): Nodeの辞書 """ res = [] for node_idx in self.node: res.append([nodes_dict[node_idx].x, nodes_dict[node_idx].y]) self.xy = np.array(res) class Mesh: """ NodeオブジェクトとElementオブジェクトをまとめておくクラス Attributes: id (int): メッシュのID(重複不可) nodes ({Node.id: Node}): Nodeの辞書 elements (list): Elementのリスト """ def __init__(self, idx, nodes_dict, elements): self.id = idx self.nodes = nodes_dict self.elements = elements self.get_element_coord() def get_element_coord(self): for elm in self.elements: elm.get_coordination(self.nodes) class Material: """ 材料特性をまとめておくクラス Attributes: E (float): ヤング率 nu (float): ポアソン比 """ def __init__(self, E, nu): self.E = E self.nu = nu class Solver: """ 有限要素法の計算を行うクラス Attributes: mesh (Mesh): Meshクラス material (Material): Materialクラス D (array 3x3): Dマトリクス """ def __init__(self, mesh, material): self.mesh = mesh self.material = material self.D = self.calc_D() def run(self): self.f, self.bc_dist_dict = self.read_boundary_cond() self.K = self.calc_K() self.d = self.solve() def calc_D(self): """ Dマトリクスを算出。 Returns: D (array 3x3): Dマトリクス """ D = np.array([[1, self.material.nu, 0], [self.material.nu, 1, 0], [0, 0, (1 - self.material.nu) / 2]]) \ * self.material.E / (1 - self.material.nu ** 2) return D def calc_B(self, elem, xi, eta): """ Bマトリクス及びヤコビアンを算出。 Args: elem (Element): 対象のElementクラス xi, eta (float): Bマトリクス算出用の座標 Returns: B (array 3x8): Bマトリクス J (array 2x2): ヤコビアン """ dndxi = np.array([- 1 + eta, 1 - eta, 1 + eta, - 1 - eta]) / 4 dndeta = np.array([- 1 + xi, - 1 - xi, 1 + xi, 1 - xi]) / 4 x = elem.xy[:, 0] y = elem.xy[:, 1] dxdxi = np.dot(dndxi, x) dydxi = np.dot(dndxi, y) dxdeta = np.dot(dndeta, x) dydeta = np.dot(dndeta, y) J = np.array([[dxdxi, dydxi], [dxdeta, dydeta]]) B = np.zeros((3, 8)) for i in range(4): Bi = np.dot(np.linalg.inv(J), np.array([dndxi[i], dndeta[i]]).T) B[0, 2 * i] = Bi[0] B[2, 2 * i + 1] = Bi[0] B[2, 2 * i] = Bi[1] B[1, 2 * i + 1] = Bi[1] return B, J def calc_Ke(self, elem): """ Keマトリクスを算出。 Args: elem (Element): 対象のElementクラス Returns: Ke (array 8x8): 要素剛性マトリクス """ gps = ((-1 / np.sqrt(3), -1 / np.sqrt(3), 1, 1), (1 / np.sqrt(3), -1 / np.sqrt(3), 1, 1), (1 / np.sqrt(3), 1 / np.sqrt(3), 1, 1), (-1 / np.sqrt(3), 1 / np.sqrt(3), 1, 1), ) Ke = np.zeros((8, 8)) for xi, eta, wi, wj in gps: B, J = self.calc_B(elem, xi, eta) Ke += wi * wj * np.dot(B.T, np.dot(self.D, B)) * np.linalg.det(J) * elem.thickness return Ke def calc_K(self): """ Kマトリクスを算出。 Returns: K (array 2node_numx2node_num): 全体剛性マトリクス """ K = np.zeros((len(self.mesh.nodes) * 2, len(self.mesh.nodes) * 2)) for elem in self.mesh.elements: Ke = self.calc_Ke(elem) for i in range(4): for j in range(4): K[2 * elem.node[i]:2 * elem.node[i]+2, 2 * elem.node[j]:2 * elem.node[j]+2] += Ke[2 * i:2 * i+2, 2 * j:2 * j+2] return K def read_boundary_cond(self): """ 境界条件を読み込み。 Returns: f (array 2node_num): 全体荷重ベクトル bc_dist_dict (dict): 全体変位ベクトルのうち、変位拘束のあるindをまとめた辞書 """ bc_dist_dict = {} f = [] for k,v in self.mesh.nodes.items(): f += v.bc_force if v.bc_dist[0] is not None: bc_dist_dict[k * 2] = v.bc_dist[0] if v.bc_dist[1] is not None: bc_dist_dict[k * 2 + 1] = v.bc_dist[1] return np.array(f), bc_dist_dict def solve(self): for i in range(len(self.mesh.nodes) * 2): if i in self.bc_dist_dict.keys(): self.K[i, :] = np.zeros(len(self.mesh.nodes) * 2) self.K[:, i] = np.zeros(len(self.mesh.nodes) * 2) self.K[i, i] = 1.0 d = np.dot(np.linalg.inv(self.K), self.f.T) return d def plot_deform(self, ratio=50): x = np.array([[node.x, node.y] for idx, node in self.mesh.nodes.items()]) x_new = x + self.d.reshape(len(self.mesh.nodes), 2) * ratio fig, ax = plt.subplots() for v in self.mesh.elements: patch = patches.Polygon(xy=v.xy, ec='black', alpha=0.3, fill=False) ax.add_patch(patch) for v in self.mesh.elements: xy_new = [(x_new[idx, 0], x_new[idx, 1]) for idx in v.node] patch = patches.Polygon(xy=xy_new, fc='red', ec='red', alpha=0.3, fill=False) ax.add_patch(patch) ax.autoscale() ax.set_aspect('equal', 'box') plt.show() def create_mesh(length, height, mesh_size, thickness): """ モデルを格子点に分割し、全ての点のNodeクラスおよびそれらを使用した4角形1次要素を作成する. ただし、モデル形状は四角形とする。 Args: length, height (float): モデルの長さ、高さ mesh_size (float): 分割したいメッシュのサイズ thickness (float): 要素の厚み(今回は全て一定とする) Returns: nodes_dict ({Node.id: Node}): 作成したNodeの辞書 elsms (list): 作成したElementクラスをまとめたリスト """ # Nodeの作成 num_mesh_len = int(length / mesh_size) num_mesh_hei = int(height / mesh_size) if num_mesh_len == 0: num_mesh_len = 1 if num_mesh_hei == 0: num_mesh_hei = 1 x = np.linspace(0, length, num_mesh_len + 1) y = np.linspace(0, height, num_mesh_hei + 1) X, Y = np.meshgrid(x, y) X = X.ravel() Y = Y.ravel() nodes_dict = {} for i, coord in enumerate(zip(X, Y)): nodes_dict[i] = Node(i, coord[0], coord[1]) # Elementの作成 node_idx = 0 elem_idx = 0 elems = [] for i in range(num_mesh_hei): for j in range(num_mesh_len + 1): if (node_idx + 1) % (num_mesh_len + 1) == 0: node_idx += 1 continue else: node_idxs = [node_idx, node_idx + 1, node_idx + num_mesh_len + 2, node_idx + num_mesh_len + 1] elems.append(Element(elem_idx, node_idxs, thickness)) node_idx += 1 elem_idx += 1 return nodes_dict, elems def plot_mesh(mesh): fig, ax = plt.subplots() for elem in mesh.elements: patch = patches.Polygon(xy=elem.xy, ec='black') ax.add_patch(patch) text_xy = np.mean(elem.xy, axis=0) ax.text(text_xy[0], text_xy[1], elem.id, fontsize=12, va='center', ha='center') for node in mesh.nodes.values(): ax.scatter(node.x, node.y, fc='black', s=100) ax.text(node.x, node.y, node.id, fontsize=8, color='white', va='center', ha='center') ax.autoscale() ax.set_aspect('equal', 'box') plt.show() MESH_SIZE = 5 LENGTH = 10. HEIGHT = 10. THICKNESS = 1. E = 208000 # ヤング率 NU = 0.27 # ポアソン比 nodes_dict, elems = create_mesh(LENGTH, HEIGHT, MESH_SIZE, THICKNESS) mesh = Mesh(0, nodes_dict, elems) material = Material(E, NU) num_mesh_len = int(LENGTH / MESH_SIZE) num_mesh_hei = int(HEIGHT / MESH_SIZE) if num_mesh_len == 0: num_mesh_len = 1 if num_mesh_hei == 0: num_mesh_hei = 1 for k, v in mesh.nodes.items(): # x変位の境界条件を設定 if v.x == 0.0: v.bc_dist[0] = 0.0 # y変位の境界条件を設定 if v.x == 0.0: v.bc_dist[1] = 0.0 # 荷重の設定 if v.x == LENGTH and (v.y == 0.0 or v.y == HEIGHT): v.bc_force = [10000 / num_mesh_hei / 2, 0.0] elif v.x == LENGTH: v.bc_force = [10000 / num_mesh_hei, 0.0] solver = Solver(mesh, material) solver.run() solver.plot_deform()
結果は以下の通りです。

メッシュをもう少し細かくすると以下のようになります。

理論値との比較は今後やるとして、見た目的にはまともに解析できてそうです。
終わりに
今回であらかた有限要素法の実装が完了しました。すごく長いプログラムになりましたが、自分でも実装してみるとブラックボックスだったFEMがだいぶ理解できた気がします。