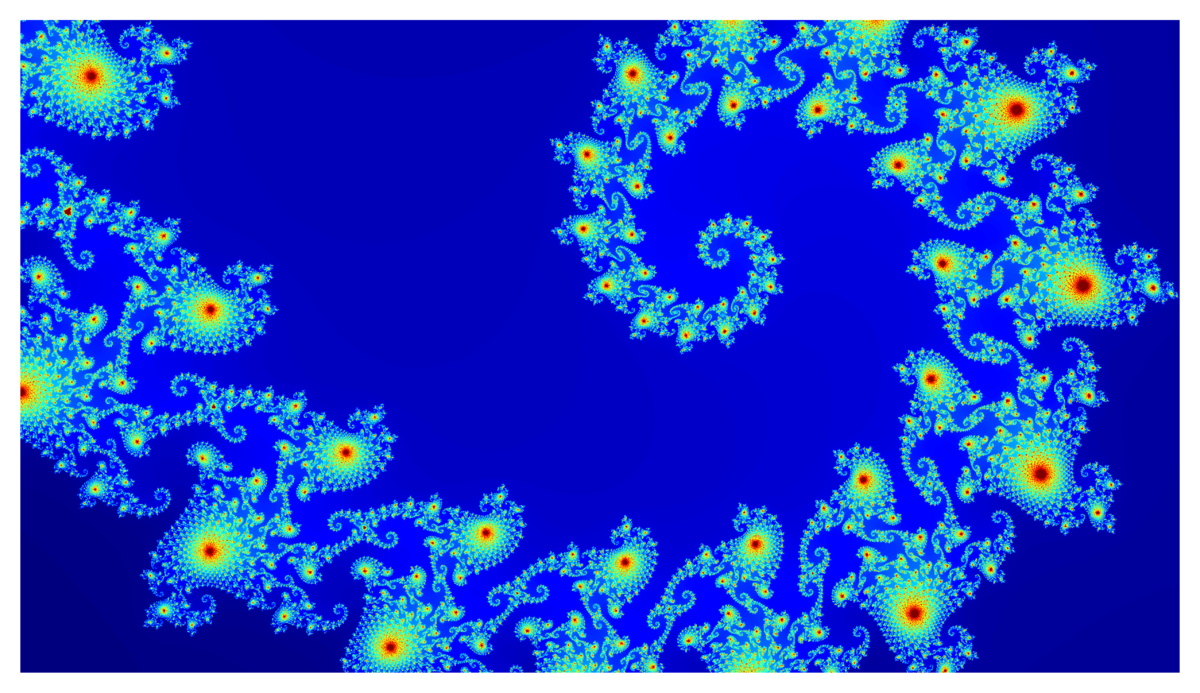
フラクタル図形といえば、で有名なマンデルブロ集合を今回は書いていきます。
マンデルブロ集合とは?
下記のような図形のことです。見たことありますか?

不思議な形はしてるけど何が面白いの?ってところですが、拡大すればするほど不思議な図形が浮かび上がってきます。
youtubeで以下の動画が人気ですね。1時間ずーっと拡大してます 笑
マンデルブロ集合の定義
すごく複雑ですが、すごく簡単な数式で定義されています。
以下に示す漸化式で定義される複素数列を考えます。
の極限で
が無限大に発散しないという条件に当てはまる複素数
の集合をマンデルブロ集合といいます。
よく見るあの形は、実数を用いて
としてx,y平面上にプロットしたものです。
色は発散までの速さを示しています。 を
増やしていく間に何回で発散したかというものです。
発散したかどうかの判定は、一度でもとなれば
は無限大に発散するという性質を利用します。
pythonで実装
漸化式での発散判定の関数
compに座標をいれてその座標における複素数
が発散するかどうか判定します。
色付けに使用したいので、出力には発散までの回数を出力させます。
def mandelbrot(n, comp): c = complex(comp[0], comp[1]) z = complex(0, 0) for i in range(n): z = z*z + c # zの絶対値が一度でも2を超えればzが発散 if abs(z) >= 2: return i return n # 無限大に発散しない場合にはnを返す
全コード
上記の関数を使って、グラフを描いてみましょう。
プロット用の関数を作り、画像としたいエリアの中心座標x_c, y_cとエリアの横幅width、
そして、画像の解像度と発散判定の繰り返し回数nを引数に入れて自由にいじって遊べるようにしております。
画像はPCの壁紙とかに使えるかなと思って16:9のアスペクト比にしています。
import numpy as np import matplotlib.pyplot as plt def mandelbrot(n, comp): c = complex(comp[0], comp[1]) z = complex(0, 0) for i in range(n): z = z*z + c # zの絶対値が一度でも2を超えればzが発散 if abs(z) >= 2: return i return n # 無限大に発散しない場合にはnを返す def plot_mand(x_c, y_c, width, resolution, n): height = width * 9 / 16 xres = resolution * 16 // 25 yres = resolution * 9 // 25 x = np.linspace(x_c - width / 2, x_c + width / 2, xres) y = np.linspace(y_c - height / 2, y_c + height / 2, yres) #実部と虚部の組み合わせを作成 X, Y = np.meshgrid(x, y) mesh = np.zeros(len(X.ravel())) for i, comp in enumerate(zip(X.ravel(), Y.ravel())): mesh[i] = mandelbrot(n, comp) mesh = mesh.reshape((yres, xres)) fig = plt.figure(dpi=600) plt.axis('off') plt.imshow(mesh, cmap="jet") fig.tight_layout() plt.show() #画像を保存 fig.savefig("mandelbrot.png", bbox_inches='tight') plot_mand(0, 0, 4.4, 4000, 50)
↓今回は実部0.0, 虚部0.0, 幅4.4, 解像度4000, 繰り返し回数50で描画しました。

マンデルブロ集合の旅
最初に示した動画みたいに、拡大していくと面白い図形が表れていくみたいです。
マンデルブロ探検家の先人たちが、名所探しみたいなものをやっていて、
名所の座標と幅等のデータがいろいろ転がってますので、試しにやってみてください。
以下ギャラリー
x_c =-0.743643135, y_c = 0.131825963, width = 0.000014628, n = 1000
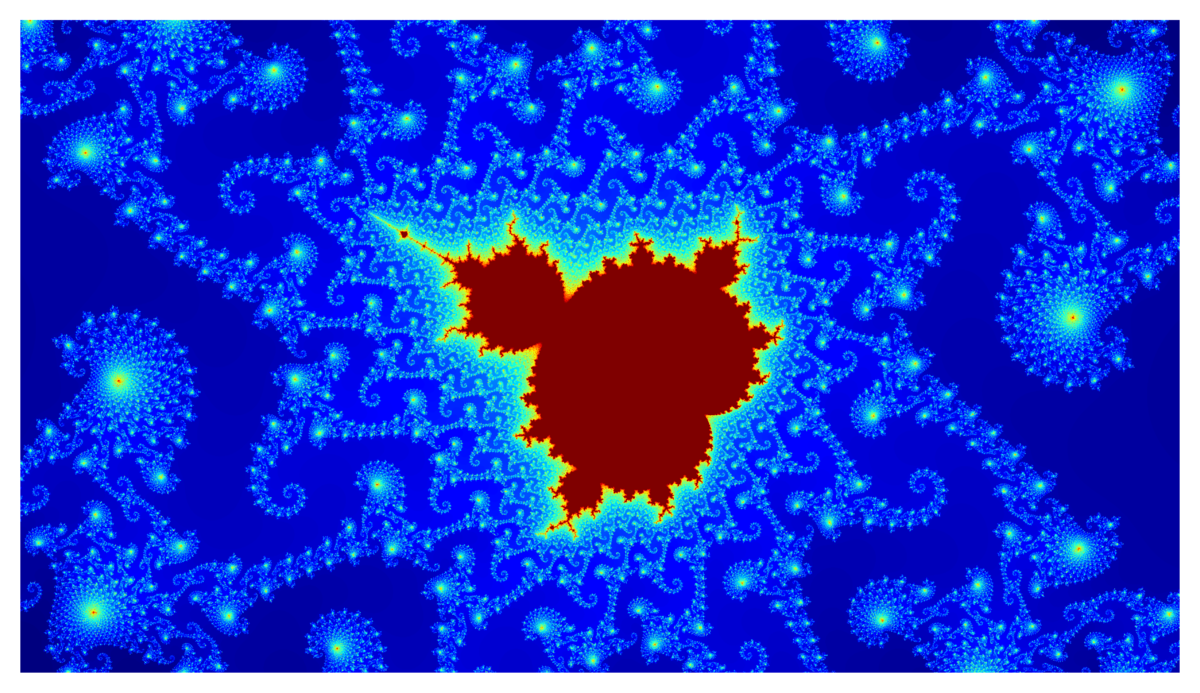
x_c =-0.7435, y_c = 0.1314, width = 0.002, n = 500