【python】運動方程式の数値解析シミュレーション入門(陽解法)

数値解析をやってみる

むかーし大学の授業でやったことを思い出しながら運動方程式の数値解析をやっていきたいと思います。
今回使うのは基本中の基本であるオイラー法とルンゲクッタ法です。
どちらも陽解法に分類され、計算が簡単なのでよく教科書とかで取り上げられてます。
陽解法とは現在の状態をもとに微小時間( $dt$ )後の状態を予測する数値解析手法です。
ではさっそくやっていきましょう。

減衰振動の運動方程式

対象として以下のシステムの数値解析を行います。

絵が雑ですいませんが、よくある外力なしの1自由度のバネーマスーダンパ系です
質量 $m$ の台車がバネ定数 $k$ のバネと減衰係数 $c$ のダンパにつながったシステムです。この台車の変位 $x$ の時間 $t$ における運動は以下の2階の常微分方程式で表すことができます。

$m\dfrac{d^2 x}{dt^2} = -c\dfrac{dx}{dt} - kx$

運動方程式の厳密解

数値解析結果が理論上の解とどの程度違うか比較したいと思います。
この方程式の理論上の厳密解は、減衰 $c$ が非常に小さい場合以下のようにあらわすことができます。

$x = e^{-\gamma t}(A_{1}\cos \omega t + A_{2}\sin \omega t)$

ここで $A_{1}, A_{2}$ は初期値によって変わる任意定数、 $\omega, \gamma$ は下記のように置いています。

$\omega = \dfrac{\sqrt{4mk - c^2}}{2m}, \gamma = \dfrac{c}{2m}$

台車の変位と速度の初期値をそれぞれ $x_{0}, v_{0}$ としたときに、上記の式は下記のように書けます。

$x = e^{-\gamma t}(x_{0}\cos \omega t + \dfrac{x_{0}\gamma + v_{0}}{\omega}\sin \omega t)$

Pythonで厳密解をプロットしてみましょう。
サンプリング周波数を100Hzとして20秒間のデータをプロットします。
初期値は $x_{0}=1, v_{0}=0$ としました。バネがめいいっぱい引っ張られている状態から台車を離す感じです。

import numpy as np
import matplotlib.pyplot as plt

# 変数の定義
m = 1
k = 5
c = 0.5
x_0 = 1
v_0 = 0
dt = 0.01

# 時間データ
t = np.arange(0, 20, dt)

# 理論解の導出
gamma = c / 2 * m
omega = np.sqrt(k / m)
x_true = np.exp(- gamma * t) * (x_0 * np.cos(omega * t) 
                          + (x_0 * gamma + v_0) / omega * np.sin(omega * t))

# プロット
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(t, x_true, label='True')
ax.set_xlabel('t')
ax.set_ylabel('x')
plt.legend(loc='best')

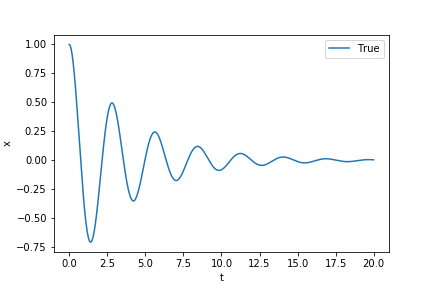
開始直後は振動しますが、時間の経過とともに振幅が小さくなっていき静止する様子がわかると思います。
では、数値解析に移りましょう。

オイラー法によるの運動方程式の数値解析

最初に書いた運動方程式を変位 $x$ と速度 $v$ で書き直すと、以下の式で表すことができます。

$\dfrac{dx}{dt} = v$

$\dfrac{dv}{dt} = -\dfrac{c}{m}v - \dfrac{k}{m}x = f(v, x)$

時刻 $t$ における変位と速度を $x_{i}, v_{i}$ としたときに、そこから微小時間後( $t + dt$ )の変位と速度( $x_{i+1}, v_{i+1}$ )を、オイラー法では以下の式で算出します。

$x_{i+1} = v_{i}dt$
$v_{i+1} = f(v_{i}, x_{i})dt$

$dt$ をめちゃくちゃ小さくすれば別ですが、簡単なだけに精度はすごく悪いです。

Pythonでオイラー法を実装する

では実装していきましょう。
最近pythonの関数の引数に関数を与えられることに気づいたので使っていきます。
まずプログラムを見やすくするために上記の $f(v, x)$ を関数にします。

# 運動方程式の関数化
def func(v, x, m=1, k=5, c=0.5):
    '''運動方程式'''
    return - c / m * v - k / m * x

続いて上記の式を参考にオイラー法を実装すると以下のようになりました。

# オイラー法による数値解析
def euler_method(t, dt, x_0, v_0, func):
    '''オイラー法'''
    x = np.zeros((len(t)))
    v = np.zeros((len(t)))
    for i in range(len(t) - 1):
        if i == 0:
            x[i] = x_0
            v[i] = v_0
            
        x[i + 1] = x[i] + v[i] * dt
        v[i + 1] = v[i] + func(v[i], x[i]) * dt
    return x

# プロット(厳密解と比較)
x_euler = euler_method(t, dt, x_0, v_0, func)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(t, x_true, label='True')
ax.plot(t, x_euler, 'r', label='Euler')
ax.set_xlabel('t')
ax.set_ylabel('x')
plt.legend(loc='best')

青の線が厳密解で、赤の線がオイラー法による解析解です。
やはり急激に速度が変わる点では誤差が大きいことがわかります。

ルンゲクッタ法によるの運動方程式の数値解析

ルンゲクッタ法はオイラー法よりは少々計算が多くなりますが、古くから使われている高精度な手法です。
ルンゲクッタ法にもいろいろと種類があるようですが、一番有名な4次のルンゲクッタ法を行います。
4次のルンゲクッタ法は微小時間後( $t + dt$ )の変位と速度( $x_{i+1}, v_{i+1}$ )は以下の式で計算します。
詳しいことは偉い人に聞いてください。

$x_{i+1} = x_{i} + \dfrac{1}{6}(k_{1x} + 2k_{2x} + 2k_{3x} + k_{4x})$

$v_{i+1} = v_{i} + \dfrac{1}{6}(k_{1v} + 2k_{2v} + 2k_{3v} + k_{4v})$

ここで、 $k$ は以下で計算します。
$k_{1x} = v_{i}dt$
$k_{1v} = f(v_{i}, x_{i})dt$
$k_{2x} = (v_{i}+k_{1v}/2)dt$
$k_{2v} = f(v_{i}+k_{1v}/2, x_{i}+k_{1x}/2)dt$
$k_{3x} = (v_{i}+k_{2v}/2)dt$
$k_{3v} = f(v_{i}+k_{2v}/2, x_{i}+k_{2x}/2)dt$
$k_{4x} = (v_{i}+k_{3v})dt$
$k_{4v} = f(v_{i}+k_{3v}, x_{i}+k_{3x})dt$

Pythonでルンゲクッタ法を実装する

上記式を参考に実装してみます。

# ルンゲクッタ法による数値解析
def runge_kutta_method(t, dt, x_0, v_0, func):
    '''ルンゲクッタ法'''
    x = np.zeros((len(t)))
    v = np.zeros((len(t)))
    for i in range(len(t) - 1):
        if i == 0:
            x[i] = x_0
            v[i] = v_0
            
        k1_x = v[i] * dt
        k1_v = func(v[i], x[i]) * dt
        
        k2_x = (v[i] + k1_v / 2) * dt
        k2_v = func(v[i] + k1_v / 2, x[i] + k1_x / 2) * dt
        
        k3_x = (v[i] + k2_v / 2) * dt
        k3_v = func(v[i] + k2_v / 2, x[i] + k2_x / 2) * dt
        
        k4_x = (v[i] + k3_v) * dt
        k4_v = func(v[i] + k3_v, x[i] + k3_x) * dt
        
        x[i + 1] = x[i] + (k1_x + 2 * k2_x + 2 * k3_x + k4_x) / 6
        v[i + 1] = v[i] + (k1_v + 2 * k2_v + 2 * k3_v + k4_v) / 6
    return x

# プロット(厳密解と比較)
x_rk = runge_kutta_method(t, dt, x_0, v_0, func)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(t, x_true, label='True')
ax.plot(t, x_rk, 'g', label='Runge-Kutta')
ax.set_xlabel('t')
ax.set_ylabel('x')
plt.legend(loc='best')